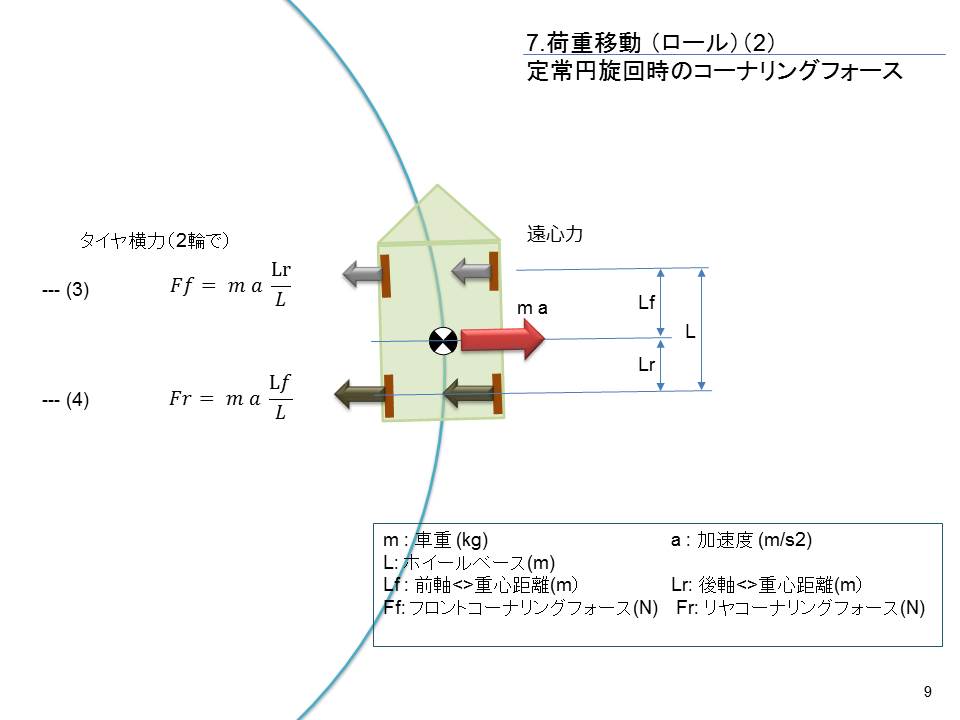
7. ＜ 定常円旋回時のタイヤ横力 ＞

旋回の話です、定常です、つまりは同じ円の上を同じ速度で旋回してる時の話です。

定常円旋回時の前後のタイヤ横力を求めるのは簡単です、遠心力と釣り合っているのですから。
タイヤ横力の総量は前々回書いた通り遠心力と同じです、これが釣り合ってないと旋回半径が変わることになっちゃいます。

ではその前後の振り分けは？ すごい簡単です、単なる重量配分の逆です。

まずは
（遠心力）＝ (タイヤ横力の総和） ---（１）
というのは上で言いました。

そして
（タイヤ横力の総和） ＝ （前2輪タイヤ横力合計）＋（後ろ2輪タイヤ横力合計） ---（２）
となります、そりゃそうですよね。

ここでタイヤ横力は重心からタイヤまでの距離をレバーとして車を回転しようとします、前輪と後輪では逆向きに回そうとしますがこれも釣り合ってないと車が回ってしまいます。
「正確には車が回る速度が変わってしまう」です、旋回中は車は“等速で“回転しているので、その話は小難しいのでいずれまた。

ということは
（前2輪タイヤ横力合計）ｘ （Lf、重心から前輪） ＝ （後ろ2輪タイヤ横力合計）ｘ （Lr、重心から後輪） ---（３）

（１）,（２）と（３）をガラガラポンすると前後輪のタイヤ横力 Lf, Lr は図のようになります。
見た通りレバーの長さの逆配分、つまりは重量配分となります。

「コーナリングフォースはタイヤスリップアングルと荷重によって変化して．．．」というのは本当ですが、そうやってタイヤが横力を発生した結果安定した旋回をし始めた時のタイヤ横力は式のようになっているということです。
コーナリングフォースをタイヤからではなく旋回の遠心力の側から見れば意外と簡単に求められちゃうのです。

さてこれを使ってロールの荷重移動に戻ります。