58c. ＜ 定常円旋回、実ロール角 ＞

前回間違ってしまったので今回はその訂正をさせていただきます。
前回モトGPのΔφが10度くらいとか書きましたがその計算はライダーのオフセットがない状態での計算式を使ってしまいました、ですのでモトGPのΔΦが１０度くらいというのは間違いです、そのすぐ前にライダーがオフセットすると実バンク角を大きくできる、つまりΔφが小さく出来ると書いていたのに、すいません。
改めてライダーオフセットのある状態でのΔφの計算をしたいと思います。
幾何で簡単に解けるのかなと思ったんですが私の幾何力では解けませんでした、状況を簡単にした場合に限って解けたのでまずはその説明をします。
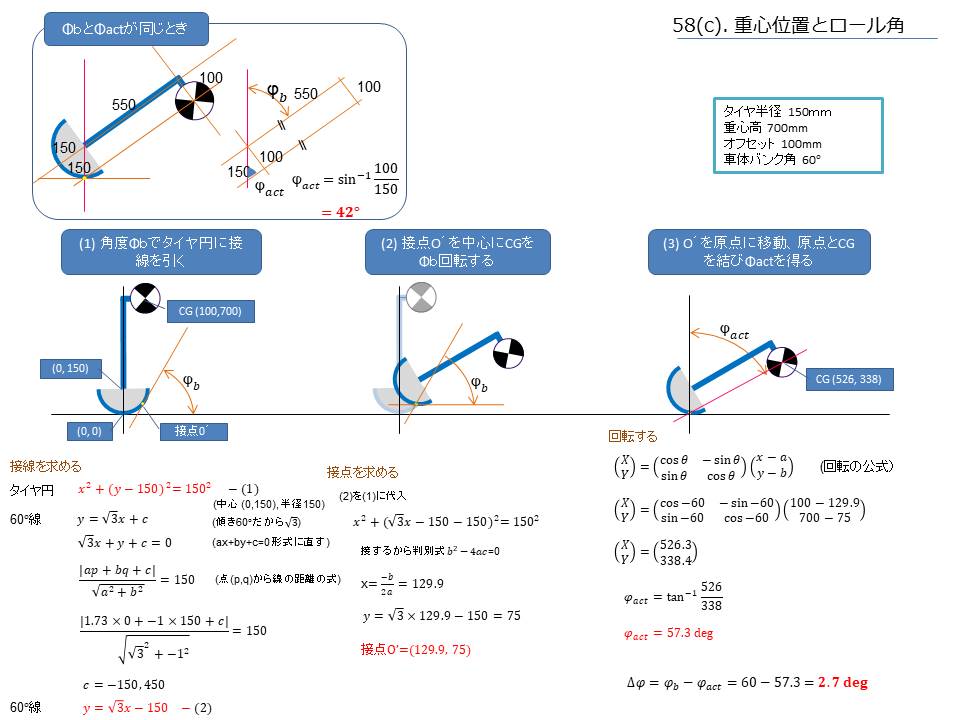
左上の囲みがそうですが車体ロール角と実ロール角が等しい状況です、この時車体ロール角の線と実ロール角の線が平行になるので簡単です、台形が出来上がりその角の直角三角形の２辺が分かっているので角度が出せます、角度は図のように42度になりました、使用した数字は前回と同じで囲みの中にある通りです。
つまり42度の時車体ロール角と実ロール角が等しくなりΔφがゼロになるということです、これがオフセットなしの時車体ロール42度だと実ロール角は33度でΔφは8.5度ですからライダーオフセットの効果は大きいですね。
これより寝かしていくと車体ロール角と実ロール角に差が出てきます。
任意の車体ロール角でのΔφを計算するのは結構面倒でした、本当は求める過程が大事なんですがそれは後回しにして結論を言うと車体ロール角60度の時実ロール角は57.3度でした、Δφは2.7度です。
かなり小さいですね！ ライダーオフセットの効果は絶大です。
Φactが60度だと横Gは1.73Gで大きすぎますが57.3度なら1.56Gでまあ納得できます。
モトGPでテレビに出るロール角は3度ほど割り引いて見るのが妥当といえると思います。
では計算の過程ですが自分でも計算できるようになってみたいとか60度じゃなくほかの角度でも計算してみたい人は読んでください。
原点中心に傾くなら簡単ですが接地点がずれていきますので厄介です、まず傾いた時の地面の線を引いてずれた接地点を求めます、そして引いた地面の線が水平になるように接地点を中心に全体を回転します
そして接地点から重心へ線を引いてその角度を求める、これが工程です。
(1) 角度Φbでタイヤ円に接線を引く
タイヤ円に今回の例でいえば60度の接線を引きます、60度傾いた時の地面の線です。
接線の傾きは60度で分かっています、角度60度の直角3角形の傾きはtan60ですね。
一方分かっていないのは切片のｃです、これを求めていきます。
点（p, q）から線までの距離の公式を使います、図にある通りです、ネットですぐ出てきます。
点はタイヤ円の中心座標(0,150)です、距離は150です。
これを入れて解くと-150と450が得られます、今回の場合-150が必要な値ですね、450はもう1本引ける円の反対側の接線の切片です。
接線の式(2) が求められました。
(2) 接点を求める
60度傾いた線とタイヤ円の接点を求めます。
円と線の両方を満足する点ですから円と線の連立2次方程式です。
タイヤ円の式は中心(0,150)で半径150ですから(1)のようになります。
(2)の接線の式を(1)の円の式に代入します。
接線ですから解は1つのはずですね（重解）、ということは判別式(b2-4ac)はゼロになりますって高校で習いましたね。
2次方程式の解も高校で習いましたね、その√の中がゼロですから x=-b/2a になり129.9 と求められました。
yはxを(2)式に入れて75と求められました。
接点O´は(129.9, 75) です。
(3) CGを接点O´を中心にΦｂ(60度)回転する
これは回転公式を使えばOKです、今回のは接点を原点に移動して回転するバージョンです、絵ではイメージしやすいよう回転して原点へ移動してますが実際は移動が先です。
(x,y)が回転前のCG、(a,b)が接点O´、Θが回転角、(X,Y)が回転後のCG座標です。
回転の公式は行列なので拒否反応が出る人もいるかもしれませんが短く書けるからそうしてるだけで展開してみればそうかと思うはずです。
結果回転後のCGは(526,338)でした。
(4) 原点とCGを結び角度を計算
これはもう簡単ですね、Φactはtan-1(Y座標/X座標) です。
そして実ロール角Φactが求められました、57.3度です。
ΔφはΦb-Φactで2.7度と求められました。
やはりどうやって解にたどり着いたかの過程が分からないとブラックボックス化してしまいちゃんと計算できてるか検証できなくなってしまいます、解法は私のやった方法だけではないでしょうしもっと簡単に解ける方法もあるでしょう、ぜひ自分で試してもらいたいもんです。