43. ＜ チェーン駆動のアンチスクォート率 （1） ＞

前回でアンチスクォート力について説明しました、アンチスクォート力は tanβ∙F で表されて駆動力と角度 βの関数です。
さてこれまでにもアンチスクォート力についてはいろいろな駆動反力支持方法によって違うことを書いてきましたが力の大きさがわかったとしても大きいのか小さいのか、どれ程のものなのかはよく分かりません。

アンチスクォート率というものについて説明します。

加速の時車体の前が軽くなって後ろが重くなります、これを前後Gによる荷重の移動といいます。
リヤは重くなるのでリヤサスペンションは縮みます、同時に駆動力によるアンチスクォート力によりサスペンションは逆に伸ばされます、２つの力が同時に掛かるわけです。
<縮める力>に対する<伸ばす力>の割合がアンチスクォート率です。

伸ばす力であるアンチスクォート力はもういいですね、縮める力つまり荷重移動量は何でしょう？ これは第1回で説明しています、車体質量ｘ重心高さ/ホイールベースです 回ごとに凡例の記号がちがっていてすいません、その時ごとに適当につけちゃうからいけないんですね、あとバイクの向きが前回と逆になってこれも見にくくてすいません、ほんとは全部左向きに書かなければいけないところでした。

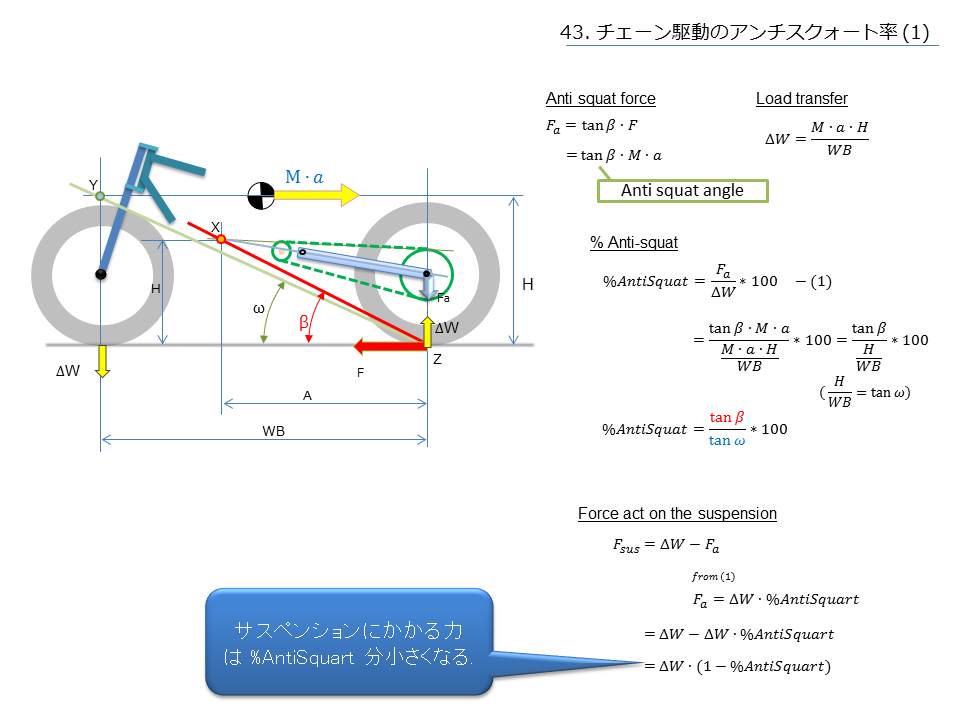
図の右上に2つの力を書いておきました見直しておいてください。
アンチスクォート率は上記2つの割合を％で表したものです、つまり伸ばす力は縮める力の何％になるか、ということです、これならアンチスクォート力の効果を表すのに分かりやすいですね。

ここで大事なのは駆動力 F＝𝑀∙𝑎 だということです、質量ｘ加速度が力ですね、これを使って式を簡単にしていきます。
こういう計算ではお決まりですが空気抵抗、転がり抵抗は無視されています、これについては後で追加の説明があります。
途中経過は見ての通りで、結果は tan𝛽と tan𝜔の比率になります。 式で考えるより図を見た方が直観的に分かりやすいですね、βとωの角度の大きさの比率になります、バイクを真横から見れば大体のアンチスクォートの度合いがそうぞうできるようになります。。
この2つの角度の関係でアンチスクォートがどれ位効いているかわかります、“０”に近ければあまりアンチスクォートは効いていない、逆に“１”に近ければアンチスクォートがよく効いているとなります。

車の話ですがランサーエボリューションのエボ３はアンチスクォート率が小さすぎで全力加速の時盛大に尻下がりになっていました、エボ４からはモデルチェンジでジオメトリーが見直されてよくなりました。これをアンチスクォート率を使って説明すると「エボ３はアンチスクォート率が小さい、エボ４は大きくなった」となります。

絵でいえばβがωに比べて小さければアンチスクォートはあまり効かず加速時尻下がりになります、βとωが同じくらいだったら縮めると伸ばすが同じくらいということになりますから伸びも縮みもしないとなります。

サスペンションの伸び縮みの関係を式にしたのがサスペンションにかかる力です、サスペンションですからね、タイヤじゃないですからね、それを言い出すと「第2回に戻る」カードが出ちゃいます。
縮める力と伸ばす力の差を求めています、サスペンションには縮める力と伸ばす力の両方が働きますから差し引きした力が実際には働くことになります、この力がサスペンションのストロークを決めるのです。


抵抗の話ですが現実の車両には転がり抵抗と空気抵抗が働きます、ですから駆動力から抵抗を引いた力が加速に使われるわけです、簡単に言うと駆動力ほどは加速しないわけです。
つまり駆動力ほどは荷重移動しない、と同じことです。
分かりやすく極端な例をあげると、車両が最高速に達してもう加速しない時を考えてください、この時加速していませんから荷重移動はゼロです、でも駆動力はどうですか？ 最大馬力の駆動力です。
駆動力全部を空気抵抗と転がり抵抗に食われちゃうから加速に回す力がないだけのことです、駆動力自体は接地面に掛かっています、タイヤは一生懸命地面を掻いているといいましょうか。
これはどういうことかというと加速はしていないから荷重移動はないけれど駆動力によるアンチスクォート力はサスペンションに掛かっている、ということです。 つまり縮める力はないけど伸ばす力はある、ということです。

２輪はダウンフォースはないものとして（最近はそうでもなくなりつつありますが）考えると直線をゼロから加速していく状況を考えると初めは尻下がりで発進から加速するでしょうけど速度が上がってきて加速が鈍くなってくるころには尻下がりじゃなくなって最高速に達した時には尻上がりになってるはずです。
まあ６速での駆動力はそんなに大きくなくて尻上が量は大したことないのかもしれませんが尻上がりか尻下がりかで言ったら尻上がりでしょう。
ダウンフォースのある４輪レーシングカーの方がなじみのある私には何とも妙な感じです、２輪は奥が深いです。