42. ＜ チェーン駆動のアンチスクォート（正解版）（2） ＞

前ページでアンチスクォート力がチェーンとスイングアームを延長して交わった点から接地点へ引いた線の角度βに比例する、と書きました。
その証明を解説します、もうこれは自動車工学ではなく数学の話です、でもこれが解けないと“どうしてそうなの？”には答えられないので。
かなり面白くないと思いますので結果だけわかりゃいいよ、という人はこの先は読まなくてもよろしいかと。

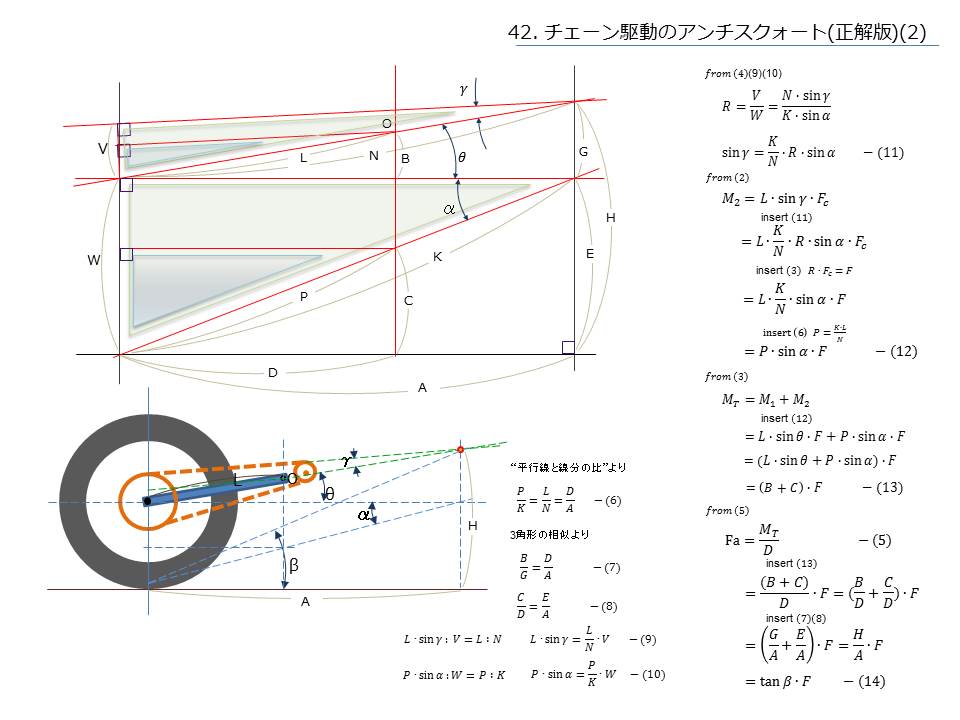
まず前のページの絵を簡略化して各辺に名前を付けました、補助線として車軸を通る水平な線、スイングアームピボットを通る垂直線等を引きました。
どの線がスイングアームやチェーンに当たるかは下の図と照らし合わせてみてください、車軸を通る水平線とKの線を引いたのがキモです。

さてまずは図から分かることを抜き出していきます、縦の垂直な線によって切られた線の比率は等しいですから（６）が分かります。
次は色を付けた2組の三角形たちは相似ですから（７）（８）（９）（１０）が分かります。
切り取られた線の比と三角形の相似は中学で習いました、忘れちゃってる人も多いと思うのですが興味のある人は検索して復習してみてください。

さあ材料はそろいました、あとは解いていくだけです、一番上から順に行きます。
前ページでギヤ比というかタイヤ径とスプロケット径の比は（４）でした、これに（９）と（１０）を代入して整理します －（１１）

前ページのチェーン力によるモーメントは（２）でした、これにさっき求めた（１１）を代入します、（３）から R・Fc＝F ですからこれも代入します さらに（６）のうち P=KL/N も代入しちゃいます。
そうして出てきたのが（１２）です、ややこしいチェーンとスイングアームの角度γとチェーン力Fcを首尾よく角度αとFに置き換えることに成功しました、これがしたかったのです。

トータルのアンチスクォートモーメントは（３）です、今求めた（１２）を代入します、そして整理すると(13)になります、だいぶすっきりしてきましたがBとCは離れたところにあってまだ分かりにくいです。

さて最終のアンチスクォート力はモーメントをスイングアーム水平長さDで割った物です（５）
（５）に（１３）を代入します、B/D+C/D っていうまだすっきりしない形ですね、ここでさらに（７）と（８）を代入します、（７）はそのまま代入できないのでB/D=G/Aに変形してから代入します。

すると分母がAで共通になり H/A という一つになりました。
H/A は何ですか? ｔanβ ですね！ ついにtanβにたどり着きました
めでたしめ でたし。