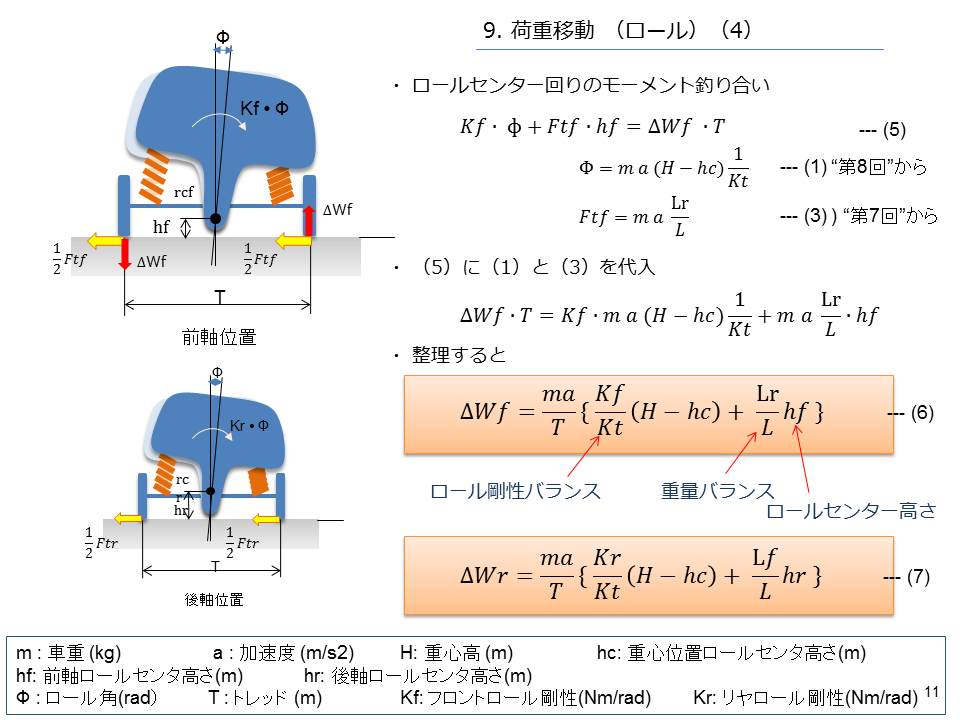
9. ＜ 荷重移動(ロール）（4） ＞

軸位置でのロールセンターまわりのモーメントの釣り合いの式を求めましょう。
式（５）です、左辺が右回り、右辺が左回りです、これらが釣り合っています。

第8回と第9回から（１）と（３）の式を持ってきました。

式（５）のΦとFtf に（）と（）を代入します、そして整理すると（）（）が得られます、これがロールの時の前後軸での荷重移動です。

ほーら荷重移動はロール剛性バランスだけじゃなくて重量バランスや重心位置と軸位置でのロールセンター高さにも影響されることが分かります。

乗用車などでは重心高に対してロールセンター高さが小さいので荷重移動はほぼロール剛性配分に比例するといってもいいでしょう。
でもレーシングカーそれもフォーミュラのように重心高が２５０ｍｍ位でロールセンターが５０ｍｍくらいだとするとロールセンター高さは無視できないことになります。

レースエンジニアの中にはステアバランス（アンダーだオーバーのことね）をロール剛性ではなくロールセンター高さで調整する人もいます。
サスペンションアームの取り付け点を変更しないといけないので時間が掛かりあんまりやる人はいませんが日本では“ジオオタク“と呼ばれてある程度います。
ロールセンター高さをサスペンション取り付け点から計算できないといけないので“難易度高し“ですね。

式（６）（７）に数字を入れれば荷重移動を計算できます、が単位は図にあるようにSI単位を使いましょう、kgだdegだを使うと単位換算で必ず訳わかんなくなって間違えます。

ロールによるステアバランスの変化はロール剛性配分変化によると思ってる人が多いですが、ロール剛性配分が変わったことによる荷重移動の配分が変わることでステアバランスが変わるのだというのが正解です。
ステアバランスを変えているのは荷重移動の前後への振り分けの違いであり、それを変えるツールがロール剛性配分であり、一部の人にとってはロールセンター高さである訳です。
まあロール剛性配分が支配的であるのは確かですけどね、数字を入れてみれば分かります。